기본적으로 아래처럼 한다.
cname <- c("x1", "x2", "x3","x4", "x5", "x6", "y")
german = read.table("c:\\data\\german1.txt", col.names = cname)
options(contrasts = c("contr.treatment", "contr.poly"))
german.object <- glm(y~.,family=binomial, data=german)
summary(german.object)
p <- predict(german.object, german, type="response")
german <- cbind(german, p)
head(german)
p는 y=1일 확률이다. 교제에서는 y=1이 불량고객이다.
> head(german)
x1 x2 x3 x4 x5 x6 y p
1 A11 6 A34 4 67 1 0 0.18170622
2 A12 48 A32 2 22 1 1 0.63312134
3 A14 12 A34 3 49 2 0 0.04812842
4 A11 42 A32 4 45 2 0 0.64393801
5 A11 24 A33 4 53 2 1 0.47102819
6 A14 36 A32 4 35 2 0 0.20127115
4 변수선택법 #
전진선택, 변수소거, 둘다
cname <- c("x1", "x2", "x3","x4", "x5", "x6", "y")
german = read.table("c:\\data\\german1.txt", col.names = cname)
#상수항만 포함한 초기모형
g.object <- glm(y~1, family=binomial, data=german)
#전진선택법
s.list <- list(upper = update(g.object, ~. +x1+x2+x3+x4+x5+x6))
step(g.object, scope=s.list, direction="forward")
#변수소거법
#s.list <- list(lower = update(g.object, ~. -x1-x2-x3-x4-x5-x6))
#step(g.object, scope=s.list, direction="backward")
#둘다
#s.list <- list(upper = update(g.object, ~. +x1+x2+x3+x4+x5+x6), lower = update(g.object, ~. -x1-x2-x3-x4-x5-x6))
#step(g.object, scope=s.list, direction="both")
결과
> step(g.object, scope=s.list, direction="forward")
Start: AIC=1223.73
y ~ 1
Df Deviance AIC
+ x1 3 1090.4 1098.4
+ x3 4 1161.3 1171.3
+ x2 1 1177.1 1181.1
+ x5 1 1213.1 1217.1
<none> 1221.7 1223.7
+ x6 1 1221.7 1225.7
+ x4 1 1221.7 1225.7
Step: AIC=1098.39
y ~ x1
Df Deviance AIC
+ x2 1 1051.9 1061.9
+ x3 4 1053.2 1069.2
+ x5 1 1085.0 1095.0
<none> 1090.4 1098.4
+ x4 1 1090.2 1100.2
+ x6 1 1090.3 1100.3
Step: AIC=1061.9
y ~ x1 + x2
Df Deviance AIC
+ x3 4 1022.6 1040.6
+ x5 1 1046.7 1058.7
<none> 1051.9 1061.9
+ x4 1 1051.5 1063.5
+ x6 1 1051.9 1063.9
Step: AIC=1040.58
y ~ x1 + x2 + x3
Df Deviance AIC
+ x5 1 1019.3 1039.3
<none> 1022.6 1040.6
+ x6 1 1022.5 1042.5
+ x4 1 1022.5 1042.5
Step: AIC=1039.27
y ~ x1 + x2 + x3 + x5
Df Deviance AIC
<none> 1019.3 1039.3
+ x4 1 1019.2 1041.2
+ x6 1 1019.3 1041.3
Call: glm(formula = y ~ x1 + x2 + x3 + x5, family = binomial, data = german)
Coefficients:
(Intercept) x1A12 x1A13 x1A14 x2
0.66510 -0.53186 -1.07608 -1.89880 0.03434
x3A31 x3A32 x3A33 x3A34 x5
-0.09915 -0.94696 -0.93433 -1.52607 -0.01277
Degrees of Freedom: 999 Total (i.e. Null); 990 Residual
Null Deviance: 1222
Residual Deviance: 1019 AIC: 1039
>
최종적으로 glm(formula = y ~ x1 + x2 + x3 + x5, family = binomial, data = german) 가 선택되었다. AIC가 가장 적은 모델이 선택된다.
참고: AIC (
![[http]](/moniwiki/imgs/http.png)
출처(http://blog.naver.com/pinokio129?Redirect=Log&logNo=80018702687))
AIC 통계량
최적 모형을 결정하는 경우 모형의 설명능력과 모형의 절약성을 고려해야 함.
모형의 설명능력은 우도(likelihood)로서 측정될 수 있으며,
모형의 절약성은 복잡한 모형 보다는 간결한 모형이 선호되어야 한다는 것으로
추정 계수의 數가 많은 것에 대해 벌칙을 가함으로써 고려될 수 있다.
그러나 모형의 설명력과 절약성은 상충되는(trade-off)기준으로서,
왕왕 복잡한 모형이 설명력이 큰것을 발견 할 수 있다.
따라서 두 판단기준을 함께 고려한 선택규준이 필요하게 된다.
그것이 바로 정보기준 접근법으로 Akailke에 의하여 개발된
Akaike Information Criterion(AIC)이다.
AIC = -2 log L +2n
여기서 'n': 파라미터 수를 나타내며, 'log L'은 대수우도(log-likelihood).
※ Akailke에 의하면 AIC통계량의 값이 최소가 되는 모형을 채택하여야 된다
D(Deviance)는 일반화된 선형 모형에서 모형의 적합도 검증 통량이다.
cname <- c("x1", "x2", "x3","x4", "x5", "x6", "y")
german = read.table("c:\\data\\german1.txt", col.names = cname)
options(contrasts = c("contr.treatment", "contr.poly"))
german.object <- glm(formula = y ~ x1 + x2 + x3 + x5, family = binomial, data = german)
summary(german.object)
결과
Call:
glm(formula = y ~ x1 + x2 + x3 + x5, family = binomial, data = german)
Deviance Residuals:
Min 1Q Median 3Q Max
-1.7997 -0.8007 -0.4747 0.9283 2.4241
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) 0.665099 0.476311 1.396 0.162607
x1A12 -0.531864 0.185402 -2.869 0.004121 **
x1A13 -1.076082 0.336956 -3.194 0.001405 **
x1A14 -1.898800 0.206314 -9.203 < 2e-16 ***
x2 0.034342 0.006329 5.426 5.76e-08 ***
x3A31 -0.099153 0.474942 -0.209 0.834629
x3A32 -0.946961 0.370644 -2.555 0.010622 *
x3A33 -0.934327 0.433303 -2.156 0.031061 *
x3A34 -1.526069 0.393754 -3.876 0.000106 ***
x5 -0.012765 0.007091 -1.800 0.071821 .
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
(Dispersion parameter for binomial family taken to be 1)
Null deviance: 1221.7 on 999 degrees of freedom
Residual deviance: 1019.3 on 990 degrees of freedom
AIC: 1039.3
Number of Fisher Scoring iterations: 4
숫자형 변수인 경우 분포를 보고 후보를 선택할 수 있다. (Y님이 알려준거다)
# r: 결과set
# r에서 숫자형 자료만 선별해서 plotting
# column이 숫자형인지 T/F 저장
training <- sqlQuery(conn, "select
cnt x1
, logkind x4
, genre x5
, diff_cnt x6
, diff_time x8
, gamecd x9
, reg_hh x10
, case when t <= 2 then 1 else 0 end y
from temp.dbo.out_data01
")
#install.packages("reshape")
#install.packages("ggplot2")
library("reshape")
library("ggplot2")
number_cols <- sapply(training, is.numeric)
r.lng <- melt(training[,number_cols], id="y") # id: 종속변수명.
p <- ggplot(aes(x=value, group=y, colour=factor(y)), data=r.lng)
p + geom_density() + facet_wrap(~variable,scale="free")
결과는 다음 그럼과 같다.
여기에서는 그림을 보고 x6, x8이 선택되었다.
5 odds와 logit #
승산(그림 출처 ->
여기(http://www.bisolutions.us/Credit-Risk-Evaluation-of-Online-Personal-Loan-Applicants-A-Data-Mining-Approach.php))
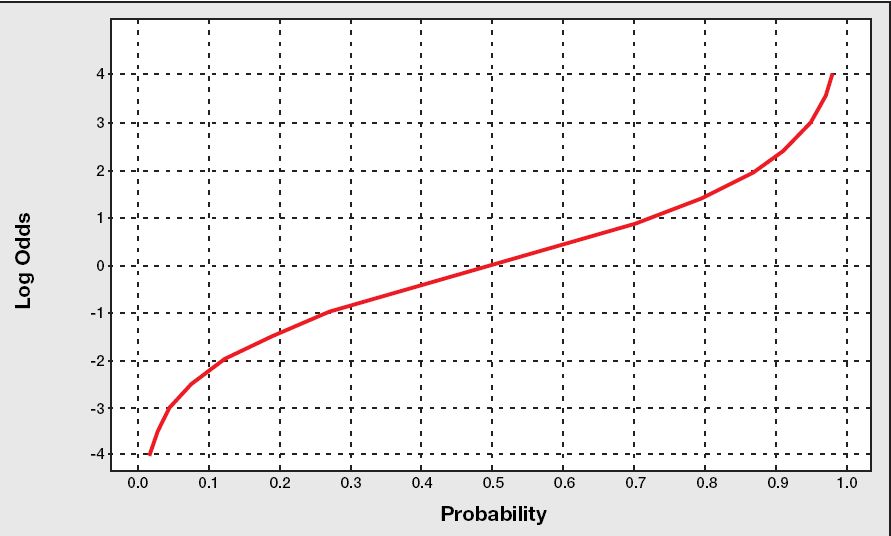
로짓(그림 출처 ->
여기(http://www.bisolutions.us/Credit-Risk-Evaluation-of-Online-Personal-Loan-Applicants-A-Data-Mining-Approach.php)) = log와 odds를 합친말 = log(1/(1-p))
pred <- predict(german.object, german, type="response")
logodds <- predict(german.object, german)
german <- cbind(german, pred) #확률
german <- cbind(german, logodds) #오즈, odds
head(german)
결과
> head(german)
x1 x2 x3 x4 x5 x6 y pred logodds
1 A11 6 A34 4 67 1 0 0.18091034 -1.5101920
2 A12 48 A32 2 22 1 1 0.63503244 0.5538676
3 A14 12 A34 3 49 2 0 0.04865313 -2.9731627
4 A11 42 A32 4 45 2 0 0.64246423 0.5860757
5 A11 24 A33 4 53 2 1 0.46964395 -0.1215737
6 A14 36 A32 4 35 2 0 0.19922819 -1.3911252
2번째 Row는
| x1 | x2 | x3 | x4 | x5 | x6 | y |
| A12 | 48 | A32 | 2 | 22 | 1 | 1 |
이고, 회귀식이 다음과 같으므로
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) 0.665099 0.476311 1.396 0.162607
x1A12 -0.531864 0.185402 -2.869 0.004121 **
x1A13 -1.076082 0.336956 -3.194 0.001405 **
x1A14 -1.898800 0.206314 -9.203 < 2e-16 ***
x2 0.034342 0.006329 5.426 5.76e-08 ***
x3A31 -0.099153 0.474942 -0.209 0.834629
x3A32 -0.946961 0.370644 -2.555 0.010622 *
x3A33 -0.934327 0.433303 -2.156 0.031061 *
x3A34 -1.526069 0.393754 -3.876 0.000106 ***
x5 -0.012765 0.007091 -1.800 0.071821 .
다음과 같이 계산된다.
0.665099 -0.531864 + 48 * 0.034342 - 0.946961 -0.012765 * 22 = 0.5538676
확률은..
x <- 0.665099 -0.531864 + 48 * 0.034342 - 0.946961 -0.012765 * 22
1 / (1 + exp(-x)) #결과값 0.6350307
exp(x) / (1 + exp(x)) #결과값 0.6350307, 이게 로지스틱 모형
과 같이 계산하면 된다.
8 분류표(confusion matrix) #
#T1 <- length(german[german$y==1 & german$pred > 0.5,]$x1)
#T0 <- length(german[german$y==0 & german$pred > 0.5,]$x1)
#F1 <- length(german[german$y==1 & german$pred <= 0.5,]$x1)
#F0 <- length(german[german$y==0 & german$pred <= 0.5,]$x1)
#
install.packages("SDMTools")
library("SDMTools")
confusion.matrix(german$y,german$pred,threshold=0.5)
결과
> confusion.matrix(german$y,german$pred,threshold=0.5)
obs
pred 0 1
0 629 177
1 71 123
attr(,"class")
[1] "confusion.matrix"
| | False(실제) | True(실제) |
| False(예측) | 629 | 177 |
| True(예측) | 71 | 123 |
| 항목 | 계산 | 확률(%) |
| 정확도 (Accuracy) | (629 + 123) / (629 + 177 + 71 + 123) | 75.20% |
| 민감도 (sensitivity) | 123 / (177 + 123) | 41.00% |
| 특이도 (specificity) | 629 / (629 + 71) | 89.86% |
| 오류율 (error) | (177 + 71 ) / (629 + 177 + 71 + 123) | 24.80% |
다음과 같이 R로 계산해도 된다.
library("SDMTools")
mat <- confusion.matrix(german$y,german$pred,threshold=0.5)
mat
omission(mat)
sensitivity(mat)
specificity(mat)
prop.correct(mat)
결과
> mat
obs
pred 0 1
0 629 177
1 71 123
attr(,"class")
[1] "confusion.matrix"
> omission(mat)
[1] 0.59
> sensitivity(mat)
[1] 0.41
> specificity(mat)
[1] 0.8985714
> prop.correct(mat)
[1] 0.752
>
다음과 같이 하면 다 나온다.
> accuracy(german$y,german$pred,threshold=0.5)
threshold AUC omission.rate sensitivity specificity prop.correct Kappa
1 0.5 0.6542857 0.59 0.41 0.8985714 0.752 0.3432203
>
값에 대한 설명
- AUC(area under curve): ROC curve 아래의 면적, 숫자가 높을수록 좋다.
- omission.rate: the ommission rate as a proportion of true occurrences misidentified given the defined threshold value
- sensitivity: 1일 확률, 민감도
- specificity: 0일 확률, 특이도
- prop.correct: 모델의 정확도
- kappa statistic
- Fleiss의 판단기준..
- 신뢰도 낮다: 0.4 미만
- 신뢰도 있다: 0.4 ~ 0.6
- 신뢰도 높다: 0.6 ~ 0.75
- 신뢰도 매우 높다: 0.75 초과
참고: 최적(정확도)의 threshold 찾기
for (i in seq(0,1,0.01))
{
rs <- c(rs, accuracy(x2$t0,x2$pred,threshold=i)$prop.correct)
}
max_val = max(rs)
for (i in seq(0,1,0.01))
{
tmp <- accuracy(x2$t0,x2$pred,threshold=i)$prop.correct
if ( max_val == tmp )
{
print (paste("threshold = ", i))
}
}
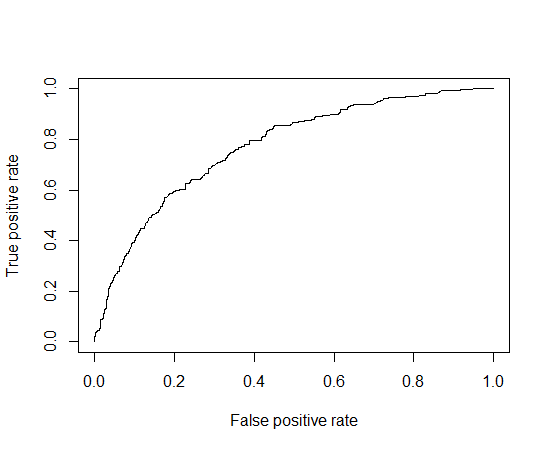
9 ROC(Receiver-Operating Characteristic curve) 곡선 #
install.packages("ROCR")
library("ROCR")
cname <- c("x1", "x2", "x3","x4", "x5", "x6", "y")
german = read.table("c:\\data\\german1.txt", col.names = cname)
options(contrasts = c("contr.treatment", "contr.poly"))
german.object <- glm(formula = y ~ x1 + x2 + x3 + x5, family = binomial, data = german)
pred <- predict(german.object, german, type="response")
logodds <- predict(german.object, german)
german <- cbind(german, pred)
german <- cbind(german, logodds)
roc = prediction(german$pred, german$y)
perf = performance(roc, "tpr", "fpr")
#"tpr"은 hit rate, "fpr"은 헛경보율(false alarm rate)
plot(perf)
#plot(perf, print.cutoff.at=seq(0,1,by=0.1))
install.packages("logistf")
library("logistf")
lr2 = logistf(y ~ x1 + x2 + x3 + x5, data = german)
summary(lr2)
결과
> summary(lr2)
logistf(formula = y ~ x1 + x2 + x3 + x5, data = german)
Model fitted by Penalized ML
Confidence intervals and p-values by Profile Likelihood
coef se(coef) lower 0.95 upper 0.95 Chisq
(Intercept) 0.64472876 0.474759083 -0.27043182 1.581359116 1.89900357
x1A12 -0.52660853 0.185120846 -0.88988344 -0.166823398 8.25198090
x1A13 -1.04548754 0.334474867 -1.72559520 -0.417128337 11.03319913
x1A14 -1.87794257 0.205266409 -2.28709164 -1.483111213 Inf
x2 0.03387929 0.006308928 0.02165981 0.046313848 29.94733537
x3A31 -0.09194231 0.473477203 -1.01911361 0.824239056 0.03855106
x3A32 -0.92696865 0.369386547 -1.66277580 -0.221680910 6.67102543
x3A33 -0.90779881 0.431809628 -1.76384501 -0.081117723 4.64170188
x3A34 -1.49870282 0.392307541 -2.27839153 -0.748208241 15.50420478
x5 -0.01252255 0.007063063 -0.02651766 0.001115517 3.23324577
p
(Intercept) 1.681899e-01
x1A12 4.070755e-03
x1A13 8.949457e-04
x1A14 0.000000e+00
x2 4.439416e-08
x3A31 8.443407e-01
x3A32 9.799279e-03
x3A33 3.120404e-02
x3A34 8.232193e-05
x5 7.215754e-02
Likelihood ratio test=200.5529 on 9 df, p=0, n=1000
Wald test = 152.8214 on 9 df, p = 0
Covariance-Matrix:
[,1] [,2] [,3] [,4] [,5]
[1,] 0.225396187 -2.116841e-02 -0.0178520944 -1.475598e-02 -1.030299e-03
[2,] -0.021168410 3.426973e-02 0.0158947775 1.663656e-02 -4.993463e-05
[3,] -0.017852094 1.589478e-02 0.1118734364 1.582290e-02 1.008258e-04
[4,] -0.014755985 1.663656e-02 0.0158228986 4.213430e-02 -6.926150e-05
[5,] -0.001030299 -4.993463e-05 0.0001008258 -6.926150e-05 3.980257e-05
[6,] -0.129133562 4.653294e-03 0.0017777035 2.271459e-03 1.822720e-04
[7,] -0.134642541 3.932850e-03 0.0010335670 1.458292e-04 2.134383e-04
[8,] -0.118628622 -2.470301e-03 0.0005935660 -5.484439e-03 -2.417103e-05
[9,] -0.126861265 4.418244e-03 0.0018526164 -2.134237e-03 2.052452e-04
[10,] -0.001743630 7.292805e-05 -0.0000437410 1.938701e-05 -1.300694e-07
[,6] [,7] [,8] [,9] [,10]
[1,] -1.291336e-01 -1.346425e-01 -1.186286e-01 -0.1268612649 -1.743630e-03
[2,] 4.653294e-03 3.932850e-03 -2.470301e-03 0.0044182436 7.292805e-05
[3,] 1.777704e-03 1.033567e-03 5.935660e-04 0.0018526164 -4.374100e-05
[4,] 2.271459e-03 1.458292e-04 -5.484439e-03 -0.0021342366 1.938701e-05
[5,] 1.822720e-04 2.134383e-04 -2.417103e-05 0.0002052452 -1.300694e-07
[6,] 2.241807e-01 1.258971e-01 1.240776e-01 0.1263132224 -8.388392e-05
[7,] 1.258971e-01 1.364464e-01 1.240557e-01 0.1260949748 7.408724e-05
[8,] 1.240776e-01 1.240557e-01 1.864596e-01 0.1247551153 -9.031551e-05
[9,] 1.263132e-01 1.260950e-01 1.247551e-01 0.1539052064 -1.431441e-04
[10,] -8.388392e-05 7.408724e-05 -9.031551e-05 -0.0001431441 4.988686e-05
이런거도 있다.
install.packages("survey")
library("survey")
regTermTest(german.object, ~x1 + x2 + x3 + x5)
결과
> regTermTest(german.object, ~x1 + x2 + x3 + x5)
Wald test for x1 x2 x3 x5
in glm(formula = y ~ x1 + x2 + x3 + x5, family = binomial, data = german)
F = 17.2046 on 9 and 990 df: p= < 2.22e-16
p-value가 조넨 작으니까 귀무가설 지지 못함. 즉, 차이가 있음.
german1.txt) 활용![[-]](/moniwiki/imgs/plugin/arrup.png "[-]")
![[+]](/moniwiki/imgs/plugin/arrdown.png "[+]")