Contents

[-]
1 베르누이의 시행
2 이항분포
3 그래프를 통한 이항분포의 이해
4 예제:불량율이 0.1인 주조공정에서 15개의 제품을 추출했을 때, 불량품이 10개 이상일 확률
5 예제:음성 패킷 손실율 1%에서 동시에 전송할 패킷수를 결정(시뮬레이션)
6 예제:10개의 공


[edit]

1 베르누이의 시행 #

  • 양품/불량품, 남/녀, 동전 던지기(앞/뒤), 주사위 던지기(짝/홀) 등
  • 전제조건
    • 실험이 n번 동일한 시행으로 구성된다.
    • 각 시행은 두 가지 가능한 결과 중 한 가지만 나타난다.
    • 각 결과의 확률은 시행의 횟수에 관계없이 일정하다.
    • 한 시행의 결과는 다른 시행의 결과에 영향을 주지 않는다. 즉, 각 시행은 서로 독립적이다.

[edit]

2 이항분포 #

확률변수 X의 분포가 이항 분포를 따를 경우 X ~ Binomial(n,p)로 표기하며, 그 확률질량함수(PMF) 식은 다음과 같다.

binormdist01.jpg
n: 베르누이 시행의 반복횟수
p: 각 시행에서 성공할 확률(0 < p < 1)
x: n번 시행중 성공의 횟수

  • 베르누이 시행의 전제하에 p와 (1-p)가 각각 어떤 시행에서의 성공과 실패의 확률이라고 하면, n번의 독립적 시행에서 x번 성공할 확률분포
  • BINOMDIST(x,n,p,c)사용
    • x: 성공횟수
    • n: 시행횟수
    • p: 매번 시행할 때마다의 성공확률
    • c: 1 or 0(True or False)
  • 예제
    • BINOMDIST(6, 10, 0.5, FALSE): 성공확률이 0.5인 시행에서 10번 시행에 6번 성공할 확률은? 0.205078125
    • BINOMDIST(6, 10, 0.5, TRUE): 성공확률이 0.5인 시행에서 10번 시행했을 때에 6회 이하로 성공할 확률은? 0.828125
  • 평균 = 시행횟수 * 매번 시행할 때마다의 성공확률 = 기대값
  • 분산 = 시행횟수 * 매번 시행할 때마다의 성공확률 * (1-매번 시행할 때마다의 성공확률)


[edit]

3 그래프를 통한 이항분포의 이해 #

binomdist01.jpg
BINOMDIST.xlsx

매회 독립 시행의 확률은 0.5이다. 즉, 50%의 확률로 성공 또는 실패한다는 것이다. P(n=10)의 그래프를 보자. 그럼 가장 뽀족한 부분에 대항되는 x축의 값이 평균이다. P(n=10)의 경우 5 근처에 데이터가 몰려있다. P(n=50)의 경우는 평균인 25 근처에 데이터가 가장 많이 발생한 것을 볼 수 있다. 또한 이 그림은 n이 커질수록 정규분포에 근사한다는 것을 보여주고 있다.

[edit]

4 예제:불량율이 0.1인 주조공정에서 15개의 제품을 추출했을 때, 불량품이 10개 이상일 확률 #

불량율이 0.1인 주조공정에서 15개의 제품을 추출했을 때, 불량품이 10개 이상일 확률은? 1.8662E-07
  • 다음의 합
    • = BINOMDIST(10, 15, 0.1, FALSE)
    • = BINOMDIST(11, 15, 0.1, FALSE)
    • = BINOMDIST(12, 15, 0.1, FALSE)
    • = BINOMDIST(13, 15, 0.1, FALSE)
    • = BINOMDIST(14, 15, 0.1, FALSE)
    • = BINOMDIST(15, 15, 0.1, FALSE)
  • = BINOMDIST(5,15,0.9,TRUE)
  • = 1-BINOMDIST(9,15, 0.1, TRUE)

주사위를 두 번 던져 모두 1이 나올 확률은? 0.027777778
  • 주사위를 1회 던져 1이 나올 확률 = BINOMDIST(1, 2, 1/6, FALSE) = 0.277777778
  • 주사위를 2회 던져 모두 1이 나올 확률 = BINOMDIST(2, 2, 1/6, FALSE) =0.027777778

A전염병에 걸려 회복될 수 있는 확률이 0.4일 때, 15명이 병에 걸린 경우
  • 적어도 10명이 회복될 확률(10명 이상 회복할 확률)은 다음의 합: 0.033833303
    • = BINOMDIST(10, 15, 0.4, FALSE)
    • = BINOMDIST(11, 15, 0.4, FALSE)
    • = BINOMDIST(12, 15, 0.4, FALSE)
    • = BINOMDIST(13, 15, 0.4, FALSE)
    • = BINOMDIST(14, 15, 0.4, FALSE)
    • = BINOMDIST(15, 15, 0.4, FALSE)
  • 3명 ~ 8명 회복될 확률은 다음의 합: 0.877838591
    • = BINOMDIST(3, 15, 0.4, FALSE)
    • = BINOMDIST(4, 15, 0.4, FALSE)
    • = BINOMDIST(5, 15, 0.4, FALSE)
    • = BINOMDIST(6, 15, 0.4, FALSE)
    • = BINOMDIST(7, 15, 0.4, FALSE)
    • = BINOMDIST(8, 15, 0.4, FALSE)

[edit]

5 예제:음성 패킷 손실율 1%에서 동시에 전송할 패킷수를 결정(시뮬레이션) #

-- 문제 출처: 확률론, Albert Leon-Garcia 지음, 김순자, 최상방, 홍광석 옮김, 피어슨 에듀케이션
패킷 음성 전송 시스템이 있다. A도시에서 B도시로 48개의 통화를 동시에 전송할 수 있는 시스템이 있다. 하지만, 음성 패킷은 약 1/3수준으로 나머지는 무음 패킷이다. 48개의 패킷을 동시에 전송하는 것은 비효율적이다. 음성 패킷 손실율 1%(통화가 불쾌하지 않을 수준이라 가정)에서 동시에 전송할 패킷수를 결정해 보자.

음성 패킷인지 무음 패킷인지는 이항분포다. 램덤으로 이항분포를 만들어 보자.
#이항분포
set.seed(48)
packets <- c()
for(i in 1:1000){
  packets <- c(packets, sum(rbinom(48, 1, 0.333)))
}
summary(packets)

시뮬레이션 해보자.
#시뮬레이션: 음성 패킷 손신율 1%에서 동시에 보낼 수 있는 패킷수는?
#손실율: (음성패킷수 - 동시보낼패킷수) > 0
n <- length(y)
prop <- c()
x <- 1:48
for(concurrent in x){
  prop <- c(prop, sum(packets > concurrent)/n)
}

plot(x, prop)
abline(h=0.01)
cutting_point <- min(which(prop < 0.01))
abline(v=cutting_point)
text(cutting_point + 1, 0.05, cutting_point)
text(1, 0.05, 0.1)
1.png
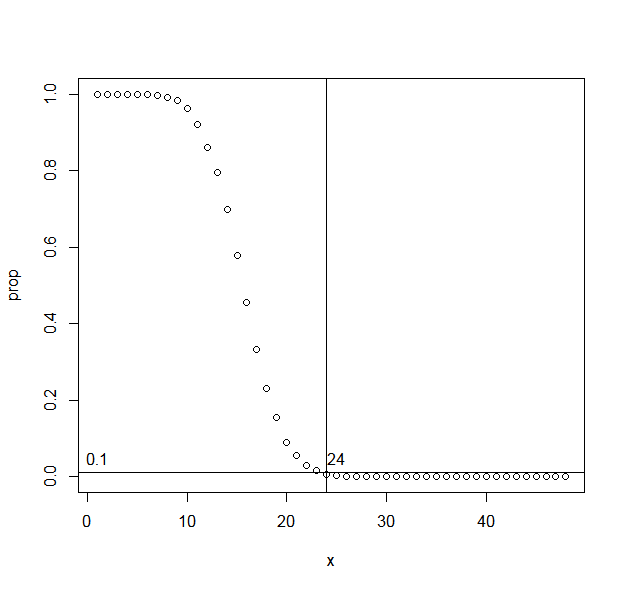
--참고: set.seed(48)을 주석처리 후 프로그램을 계속돌려보니 거의 24이며, 23, 25도 가끔씩 나왔다.

[edit]

6 예제:10개의 공 #

항아리에 공이 10개가 있다.
  • 빨간공: 4개
  • 하얀공: 6개

10번 공을 꺼냈을 때(복원 추출) 빨간공 3개를 꺼낼 확률
dbinom(3, 10, 0.4)

결과
> dbinom(3, 10, 0.4)
[1] 0.2149908

10번 공을 꺼냈을 때(복원 추출) 적어도 1개 빨간공을 꺼낼 확률 --> 1 - 빨간공을 0개 꺼낼 확률
1-dbinom(0, 10, 0.4)

결과
> 1-dbinom(0, 10, 0.4)
[1] 0.9939534

10번 공을 꺼냈을 때(복원 추출) 빨간 공을 2개 이하로 꺼낼 확률
pbinom(2, 10, 0.4)

결과
> pbinom(2, 10, 0.4)
[1] 0.1672898