3 simple regression #
독립 변수가 1개일 경우을 simple regression이라고 한다. lm()을 사용하면 간단히 할 수 있다.
lm.out <- lm(volume ~ girth, data=df)
summary(lm.out)
결과
> summary(lm.out)
Call:
lm(formula = volume ~ girth, data = df)
Residuals:
Min 1Q Median 3Q Max
-8.065 -3.107 0.152 3.495 9.587
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -36.9435 3.3651 -10.98 7.62e-12 ***
girth 5.0659 0.2474 20.48 < 2e-16 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 4.252 on 29 degrees of freedom
Multiple R-squared: 0.9353, Adjusted R-squared: 0.9331
F-statistic: 419.4 on 1 and 29 DF, p-value: < 2.2e-16
위 결과는 최소제곱법으로 최적화된 결과로 아래와 같은 회귀식을 만들 수 있다.
volume = 5.0659 * girth - 36.9435
5.0659은 가중치고, -36.9435는 바이어스다.
이것을 수동으로 해보자. 가설은 다음과 같다.
H(x) = wx + b
최적화할 함수 즉, cost function은
cost(w,b) = avg((H(x) - y)^2)
가 되겠다. 추정값(H(x))과 실제값(y)의 차이가 가장 적은 것을 찾는 것이 목적이다. 즉, cost(w,b)가 최소화되는 것이 목적이다. 제곱을 한 이유는 마이너스값이 나오지 않게 하기 위함과 추정값과 실제값의 차이가 큰 값에 패널티를 주기 위함이다. 다음과 같이 cost function을 만들고 optim() 함수를 이용해서 최적화를 해보자. 참고로 optim() 함수는 최소값을 찾는 것이 default다.
cost.f <- function(par, x, y){
w <- par[1]
b <- par[2]
H <- w*x + b
mean((H - y)^2)
}
result <- optim(par = c(0, 0), cost.f, x = df$girth, y = df$volume)
result
결과
> result
$par
[1] 5.066008 -36.945325
$value
[1] 16.91299
$counts
function gradient
103 NA
$convergence
[1] 0
$message
NULL
위 결과를 보면
- w = 5.066008
- b = -36.945325
로 최적화했다. 위 lm() 함수의 결과인 volume = 5.0659 * girth - 36.9435와 거의 같다.
4 multi regression #
독립 변수가 2개 이상인 경우를 multi regression이라고 한다. multi regression도 마찬가지로 lm() 함수를 이용하는 것과 cost function을 만들어 최적하는 방법을 써보자. 먼저 lm() 함수를 이용하면 다음과 같은 결과를 얻을 수 있다.
lm.out <- lm(volume ~ girth + height, data=df)
summary(lm.out)
결과
> summary(lm.out)
Call:
lm(formula = volume ~ girth + height, data = df)
Residuals:
Min 1Q Median 3Q Max
-6.4065 -2.6493 -0.2876 2.2003 8.4847
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -57.9877 8.6382 -6.713 2.75e-07 ***
girth 4.7082 0.2643 17.816 < 2e-16 ***
height 0.3393 0.1302 2.607 0.0145 *
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 3.882 on 28 degrees of freedom
Multiple R-squared: 0.948, Adjusted R-squared: 0.9442
F-statistic: 255 on 2 and 28 DF, p-value: < 2.2e-16
이제 cost function을 만들어야하는데, 문제는 독립변수가 n개 생겨 다음과 같이 hypothesis가 복잡해졌다는 것이다.
H(x) = w1x1 + w2x2 + ... + b
이것을 단순화시키려면 대수적으로 접근해야하는데, 이것을 행렬로 취급하면 쉬워진다. 즉,
H(X) = WX + b
와 같이 대문자 W와 대문자 X를 행렬로 취급하여 H()를 만들면 simple regression과 같이 생각할 수 있게 된다. b도 행렬 X에 포함시켜 더욱 단순하게
H(X) = WX
와 같이 만들 수 있다. R로 cost function을 만들기 전에 우선 b를 데이터셋에 포함시키는데, 1로 세팅하면 된다.
b <- 1
tmp <- cbind(b, df)
optim() 함수의 par 파라미터는 초기값을 주는 것인데 행렬의 곱(inner product)을 하려면 수학적 규칙을 맞춰야 한다. 예를 들면,
M1•M2를 하려면 M1(3x
2)와 M2(
3x2) 볼드체 부분(M1의 행수와 M2의 열수가 같아야 함)이 같아야만 되는 수학적 규칙이 있다. 그러므로 위 M1•M2는 할 수 없다. 위 예제의 데이터는 31행 3열(girth, height, b)이고 초기값은 3개가 입력되므로 3행 1열로 만들면 행렬의 곱을 할 수 있게 된다. R에서 행렬의 곱은 %*% 연산자를 쓰면 되므로 다음과 같이 cost function을 작성하면 된다.
cost.f <- function(par, X, y){
W <- as.matrix(par)
X <- as.matrix(X)
mean((X%*%W - y)^2)
}
cost function을 작성했으니 이제 최적화 해보자.
result <- optim(par = c(0, 0, 0), cost.f, X = tmp[1:3], y = tmp[4])
result
결과
> result
$par
[1] -57.9996505 4.7082120 0.3394336
$value
[1] 13.61037
$counts
function gradient
238 NA
$convergence
[1] 0
$message
NULL
결과를 보면 lm() 함수와 거의 유사하다.
lm() 함수는 최소제곱법으로 이상치에 취약하다. lm()함수를 쓰면 다음과 같은 결과를 얻는다.
lm.out <- lm(y~x, data=mydata)
plot(mydata)
abline(lm.out, col="red")
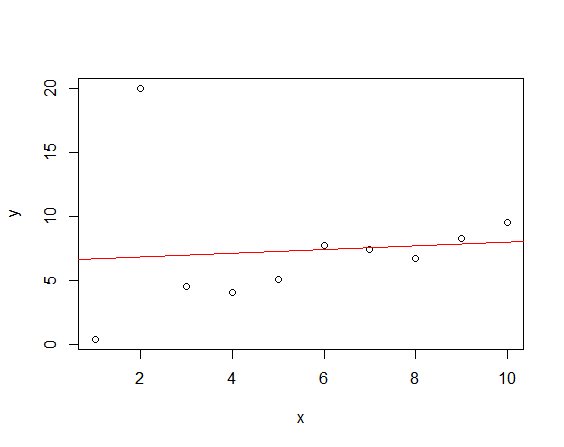
최소제곱법 말고 다른 방법을 사용해보도록 하자. 실제값과 추정치의 차이에 제곱을하여 차이가 크면 패널티를 줬지만, 여기에서는 평균 절대 편차(MAD, mean absolute deviation)로 패널티를 주지 말아보자.
cost.f <- function(par, x, y){
w <- par[1]
b <- par[2]
H <- w*x + b
mean(abs(H - y))
}
result <- optim(par = c(0, 0), cost.f, x = mydata$x, y = mydata$y)
result
결과
> result
$par
[1] 0.8849192 0.7047651
$value
[1] 2.37167
$counts
function gradient
249 NA
$convergence
[1] 0
$message
NULL
그림으로 비교해보자.
plot(mydata)
abline(lm.out, col="red")
abline(a = result$par[1], b = result$par[2], col = "blue")
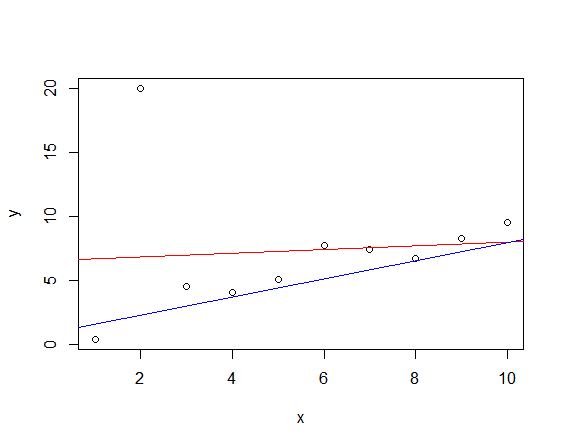
뭔가 lm() 함수를 쓴 것보다 괜찮아 보이긴 한다. 하지만, 만족스럽지는 않다.
참고로 robust regression의 결과는 다음과 같다. black line이 rlm()의 결과다.
library(MASS)
rlm.out <- rlm(y~x, data=mydata)
abline(rlm.out)
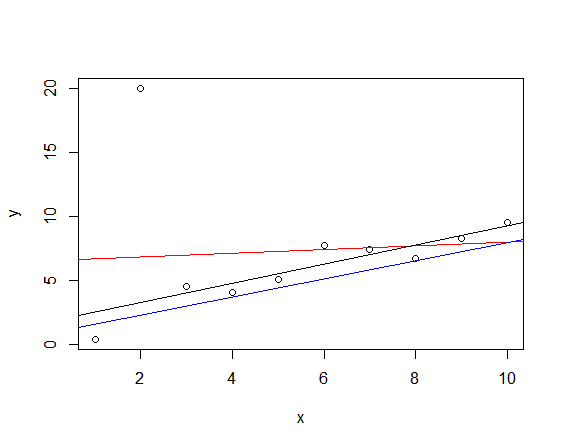
음.. 좋다. 잘 fitting됬다.